Process Reward Models
Pushing the frontier of open-source test-time scaling
Training Process Reward Models in axolotl
We’ve introduced support for fine-tuning Process Reward Models (PRMs) in axolotl. PRMs are a type of reward model that are trained on stepwise-supervision datasets, where each reasoning step is labeled for correctness. PRMs are particularly useful as a verifier for improving the outputs of language models at inference-time, and can also be used to provide fine-grained rewards for reinforcement-learning based fine-tuning.
Alongside releasing PRM fine-tuning capabilities, we’ve also produced cleaned and formatted PRM datasets, and demonstrated how you can use these datasets to fine-tune PRMs with competitive performance. Check out our PRM collection on Hugging Face Hub!
Getting started
It’s easy to kick-off a PRM training job using axolotl in a few simple steps. Firstly, we recommend formatting your data in the stepwise-supervision format:
{
"prompt": "Which number is larger, 9.8 or 9.11?",
"completions": ["The fractional part of 9.8 is 0.8, while the fractional part of 9.11 is 0.11.", "Since 0.11 is greater than 0.8, the number 9.11 is larger than 9.8."],
"labels": [True, False]
}
Where prompt indicates the initial problem, completions is a list of N reasoning steps, and labels is a list of N boolean labels indicating the correctness of each reasoning step. You’ll neeed to update your config as follows:
# prm.yaml
base_model: Qwen/Qwen2.5-3B
model_type: AutoModelForTokenClassification
num_labels: 2
process_reward_model: true
datasets:
- path: your_dataset_here
type: stepwise_supervised
step_separator: "\n\n"
max_completion_length:
train_on_last_step_only: false
splt: train
val_set_size: 0.01 # optionally, remove this to speed up training
evals_per_epoch: 10
One field to look out for here is step_separator. PRMs work by predicting the correct label for a given reasoning step - step_separator helps us correctly mark the end of one step and the beginning of the next step. You should choose this to be a string which is not usually present in the model’s vocabulary - we’ve seen variations of “\n\n\n\\n\\n...”, and also unique tokens such as ки.
Finally, kick off your training job!
axolotl train prm.yamlIf you’d like to learn more about PRMs, and how you might go about using them to improve the outputs of a language mode at inference-time, read on!
Reward modelling
Let’s use the term outcome reward models (ORMs) to refer to reward models which are trained on a single label based on the outcome of a series of interactions. The label is typically a binary indicator of whether the interaction was good or bad, and the ORM is optimized to correctly label the outcome of a given interaction.
The key innovation of PRMs is their ability to provide step-by-step feedback during the reasoning process. To achieve this, PRMs are trained on stepwise-supervision datasets where each reasoning step is labeled for correctness. A step is typically labeled as correct if it’s part of a reasoning step that leads to the right answer, though labelling schemas can vary across datasets. In contrast to ORMs, PRMs are trained to correctly label the correctness of each step in a reasoning process, rather than the outcome of an series of interactions.
Great! What can I do with my reward models?
Excellent question. Reward models are primarily used to improve the performance of a baseline auto-regressive language model. This is commonly done in two ways:
As a component of fine-tuning language models using Reinforcement Learning from Human Feedback (RLHF). RLHF aims to steer the behavior of models towards human preferences. To effectively scale this process to massive models, reward models are trained as powerful proxies for human preferences. In reinforcement-learning training paradigms, PRMs can be used to provide more granular feedback than ORMs for training reasoning models.
As verifiers for improving the outputs of language models at inference-time. This makes PRMs particularly appealing for scaling test-time inference with language models, as they can be used to verify the correctness of each step in a chain of thought reasoning process using strategies such as Best-of-N sampling or beam search.
Dataset Formats and Available Data
We’ve processed existing process supervision math-oriented datasets into a standardized format which can be used out-of-the-box with axolotl.
PRM800K: A process supervision dataset based on reasoning steps collected from the MATH dataset, and open-sourced in the Let’s Verify Step-by-Step paper comprising two phases:
axolotl-ai-co/prm800k_phase_1, which represents roughly 5% of the data collected as part of the paper, and was primarily used to seed the large-scale generation process for the second phase. The step-level labels in this dataset may be less reliable than those in the second phase.
axolotl-ai-co/prm800k_phase_2, which may include higher quality step-level labels due to additional quality control and a streamlined data collection process.
Math-Shepherd: Another math-oriented process superivison dataset introduced in the Math-Shepherd paper, generated from the MATH and the GSM8K datasets. Available at axolotl-ai-co/Math-Shepherd.
RLHFFLow: Datasets from the RLHFFLow Reward Modelling repository, comprising reasoning traces also generated from the MATH and the GSM8K datasets using two different models, and automatically labelled using the “hard estimation” strategy described in Figure 2. of the Math-Shepherd paper.
axolotl-ai-co/Mistral-PRM-Data which was generated from Mistral-7B model fine-tuned on MetaMath.
axolotl-ai-co/Deepseek-PRM-Data, which was generated from Deepseek-Math-7B-Instruct.
End-to-end example
Training
To help illustrate how you might use this feature, we’ve trained axolotl-ai-co/Qwen2.5-Math-PRM-7B and demonstrated competitive performance on a process reward model benchmark and during test-time reasoning. Let’s walk through our process of training, evaluating, and then using our model for scaling test-time reasoning.
We used Qwen/Qwen2.5-Math-7B-Instruct as our base model, and trained the PRM on a mixture of the PRM800K and Math-Shepherd datasets we described above - our config file is available in the cookbook repository. In our initial experiments, we also explored including the RLHFFlow datasets, but found that they did not demonstrate significant improvement over the significantly extended training time. In other experiments, we also found that the strong math-specific fine-tuning in the base Qwen2.5-Math-7B-Instruct model substantially improved downstream performance over training from a non-math specific base model.
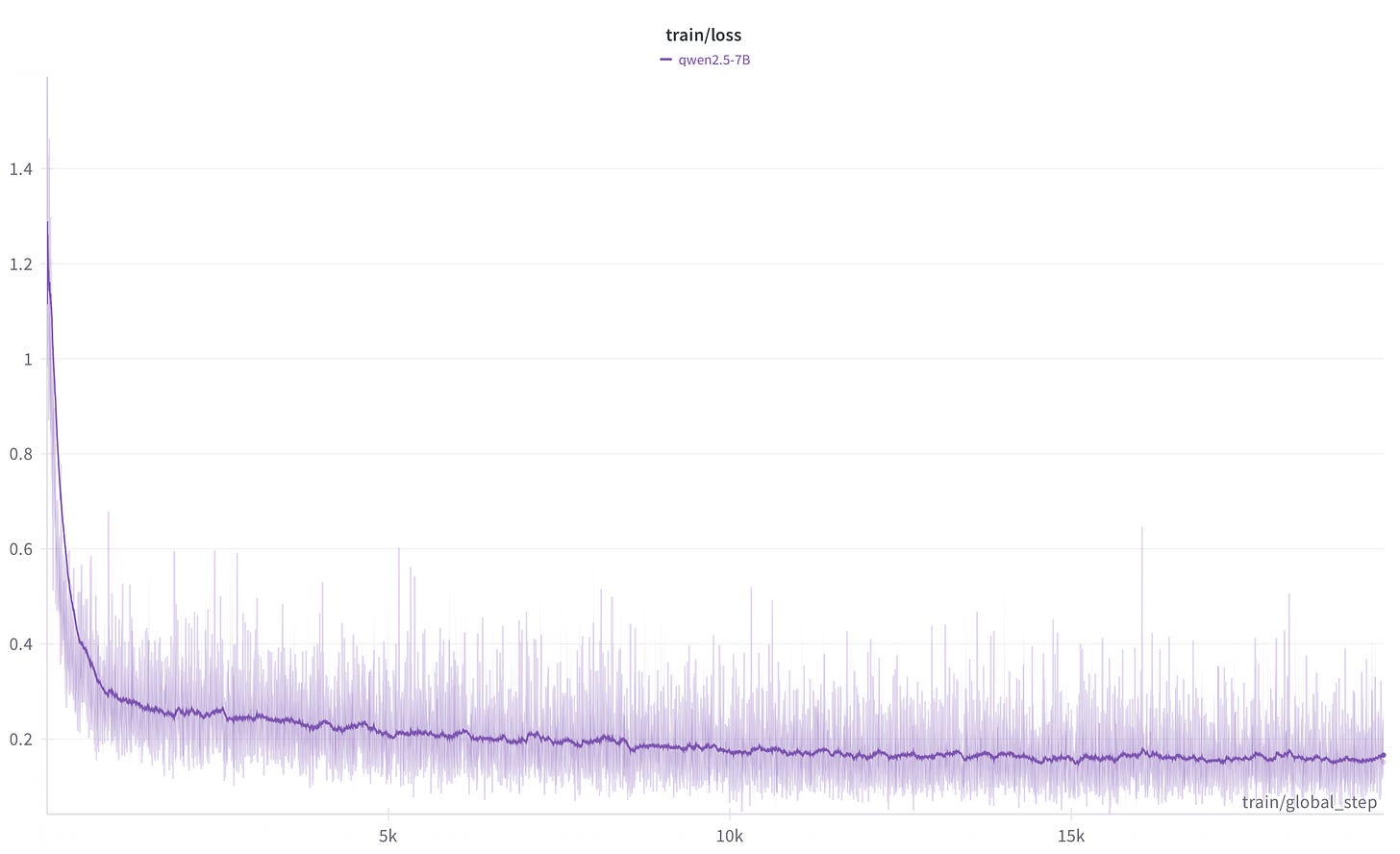
Our model was trained on 6 A100 80GB GPUs for a single epoch, with a maximum sequence length of 4096, and taking ~80 hours to complete. As above, we simply executed axolotl train prm.yaml to kick off training with our config file! If you’re following along and using Weights and Biases, you should see a training curve like this:
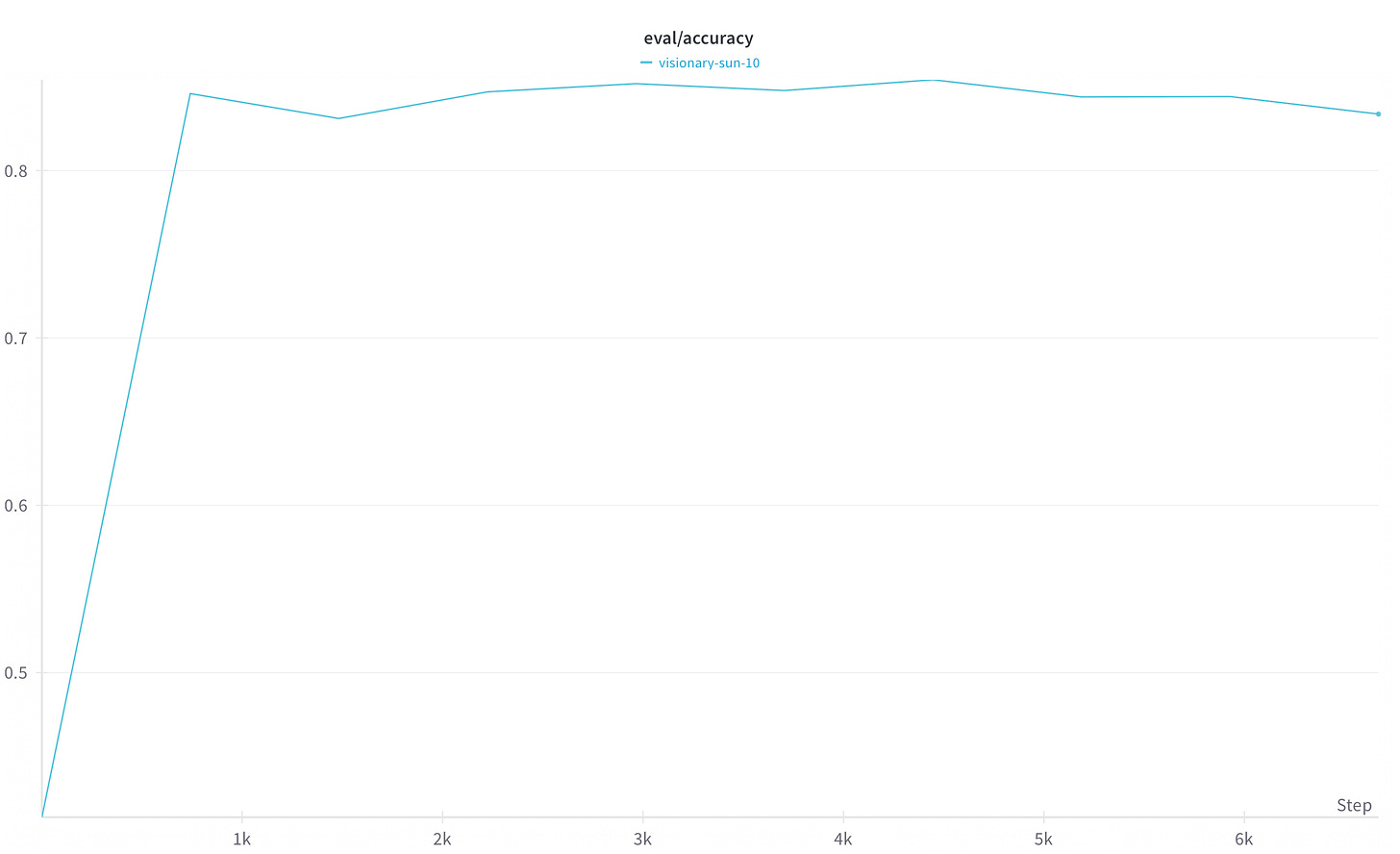
When starting out training your own models, it’s helpful to set val_set_size in your config, or to add eval_datasets to monitor the downstream accuracy of your model:
An accuracy of 0.5 indicates that your reward model is no better than random chance at correctly classifying the labels for each reasoning step - look out for this metric when experimenting with your own datasets and models.
Evaluation
To make it easy to evaluate and use your trained PRMs, we’ve included scripts in the accompanying cookbook for this blogpost. To get started, clone the repository and ensure you have a Python environment with an up-to-date version of transformers and vllm:
git clone https://github.com/axolotl-ai-cloud/axolotl-cookbook.git
cd axolotl-cookbook/prm
pip install transformers vllmProcessBench
ProcessBench is a benchmark for directly evaluating the ability of PRMs to verify the correctness of reasoning steps on several math-oriented tasks: the MATH, GSM8K, OlympiadBench, and Omni-MATH test sets.
Let’s evaluate our trained PRM on ProcessBench (note - in this example we use 8 GPUs):
torchrun --nproc_per_node=4 eval_process_bench.py --model axolotl-ai-co/Qwen2.5-Math-PRM-7B -b 24 -w 8 -s "\n\n"You should see something similar to the following output:
GSM8K:
err corr F1
----- ------ ----
55.5 98.4 71.0
MATH:
err corr F1
----- ------ ----
49.8 91.9 64.6
OlympiadBench:
err corr F1
----- ------ ----
31.2 87.3 46.0
Omni-MATH:
err corr F1
----- ------ ----
24.6 87.1 38.3
Average F1 across datasets: 50.0Best-of-N Sampling
Let’s see how we can use our PRM to improve the outputs of a language model at test-time on a downstream task. Best-of-N (BoN) sampling is a simple technique that uses a reward model to score multiple completions for the same prompt, and selects the completion with the highest score.
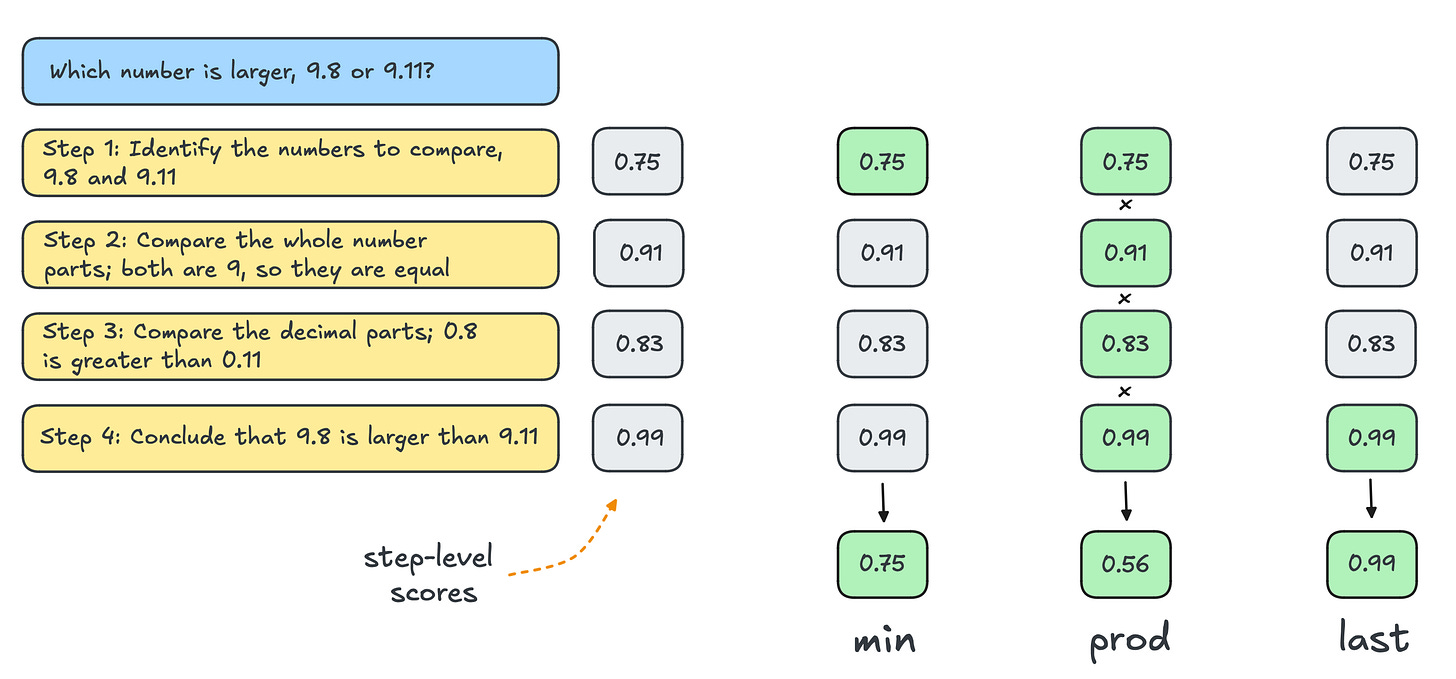
This is where your trained PRM can really shine. Instead of providing a single score for an entire solution, PRMs are able to provide a step-wise score for each reasoning step in a chain of thought process, which we can aggregate in a number of ways to produce a single score which can select the completion with the most plausible reasoning trace.
PRMs can be used as a verifier for scaling test-time reasoning. In this example, a PRM evaluates the correctness of each reasoning step. We can consider reducing the step-wise scores to a single score by using the minimum score (left), the product of all scores (middle), or the score for the final step (right). Source: Scaling test-time compute, Beeching et. al, 2024
Let’s take a look at another script in the cookbook which uses vLLM to perform BoN sampling using the “product” strategy (to mirror the setting used by by the Qwen team for Qwen2.5-Math-PRM-7B). In this example we’ll be improving the outputs of Qwen2.5-1.5B-Instruct on three example problems from the MATH-5O0 dataset. First, let’s set a baseline by using —-n 1, which simply samples from the base model without using BoN:
python bon.py --base_model Qwen/Qwen2.5-1.5B-Instruct --prm_model axolotl-ai-co/Qwen2.5-Math-PRM-7B --n 1 --num_gpus 2================================================================================
Problem: Define \[p = \sum_{k = 1}^ \infty \frac{1}{k^2} \quad \text{and} \quad q = \sum_{k = 1}^\infty \frac{1}{k^3}.\]Find a way to write \[\sum_{j = 1}^\infty \sum_{k = 1}^\infty \frac{1}{(j + k)^3}\] in terms of $p$ and $q.$
Predicted answer (BoN): To solve the given problem, we need to express the double sum \(\sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3}\) in terms of \(p\) and \(q\).
First, let's analyze the inner sum \(\sum_{k=1}^\infty \frac{1}{(j+k)^3}\). This sum can be written as:
\[
\sum_{k=1}^\infty \frac{1}{(j+k)^3}
\]
We can change the order of summation. Instead of summing over \(k\) first, we sum over \(j\) first. For a fixed \(j\), \(k\) ranges from 1 to \(\infty\). When \(j\) is fixed, \(k\) can be written as \(j + (n-j)\) where \(n\) is an integer. So, the sum becomes:
\[
\sum_{k=1}^\infty \frac{1}{(j+k)^3} = \sum_{j=1}^\infty \sum_{n=1}^\infty \frac{1}{(n)^3} = \sum_{j=1}^\infty \sum_{n=1}^\infty \frac{1}{n^3}
\]
This is exactly \(q\). So we have:
\[
\sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3} = \sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3} = q
\]
Now, we need to express \(q\) in terms of \(p\) and \(q\). Recall that:
\[
p = \sum_{k=1}^\infty \frac{1}{k^2}
\]
We need to find a way to express \(q\) in terms of \(p\). Notice that:
\[
\sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3} = \sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{j^3} \cdot \frac{1}{k^3} = \left( \sum_{j=1}^\infty \frac{1}{j^3} \right) \left( \sum_{k=1}^\infty \frac{1}{k^3} \right) = p \cdot q
\]
Thus, we have:
\[
q = \frac{p}{p} = \frac{p}{q}
\]
So, the expression for \(\sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3}\) in terms of \(p\) and \(q\) is:
\[
\boxed{q}
\]
Correct Answer: p - q
================================================================================
Problem: A regular hexagon can be divided into six equilateral triangles. If the perimeter of one of the triangles is 21 inches, what is the perimeter, in inches, of the regular hexagon?
Predicted answer (BoN): ## Step 1: ##
To solve this problem, we need to understand the relationship between the side length of the equilateral triangle and the side length of the regular hexagon it's divided into.
## Step 2: ##
Given that the perimeter of one equilateral triangle is 21 inches, we know that the perimeter of a regular hexagon composed of six such equilateral triangles is simply 6 times the perimeter of one triangle because all sides of the hexagon are equal in length and they come from equilateral triangles.
Therefore, the perimeter of the hexagon is 6 * 21.
## Step 3: ##
Calculating the perimeter of the hexagon, we get 6 * 21 = 126 inches.
## Step 4: ##
Thus, the final answer is 126 inches.
Therefore, the perimeter of the regular hexagon is $\boxed{126}$.
Correct Answer: 42
================================================================================
Problem: The expression $2\cdot 3 \cdot 4\cdot 5+1$ is equal to 121, since multiplication is carried out before addition. However, we can obtain values other than 121 for this expression if we are allowed to change it by inserting parentheses. For example, we can obtain 144 by writing \[ (2\cdot (3\cdot 4)) \cdot (5+1) = 144. \]In total, how many values can be obtained from the expression $2\cdot 3\cdot 4 \cdot 5 + 1$ by inserting parentheses? (Note that rearranging terms is not allowed, only inserting parentheses).
Predicted answer (BoN): To solve the problem of how many values can be obtained from the expression \(2 \cdot 3 \cdot 4 \cdot 5 + 1\) by inserting parentheses, we need to consider all possible ways to insert parentheses and evaluate the expression for each case.
Given the expression \( (a \cdot (b \cdot (c \cdot d) + e)) + f \), we need to evaluate it for all possible placements of parentheses.
### Step-by-Step Solution:
1. **Evaluate without parentheses:**
\[
2 \cdot 3 \cdot 4 \cdot 5 + 1 = 120 + 1 = 121
\]
2. **Evaluate with one set of parentheses:**
- \( (2 \cdot (3 \cdot 4) \cdot 5 + 1) \)
- \( 2 \cdot ( (3 \cdot 4) \cdot 5 + 1) \)
- \( (2 \cdot 3) \cdot (4 \cdot 5) + 1 \)
- \( (2 \cdot 3) \cdot ( (4 \cdot 5) + 1) \)
- \( 2 \cdot (3 \cdot (4 \cdot 5) + 1) \)
- \( 2 \cdot ((3 \cdot 4) \cdot 5) + 1 \)
3. **Evaluate with two sets of parentheses:**
- \( ((2 \cdot 3) \cdot (4 \cdot 5)) + 1 \)
- \( (2 \cdot ((3 \cdot 4) \cdot 5)) + 1 \)
- \( ((2 \cdot 3) \cdot (5 \cdot 4)) + 1 \)
- \( (2 \cdot (3 \cdot (4 \cdot 5))) + 1 \)
- \( 2 \cdot ( (3 \cdot (4 \cdot 5)) + 1) \)
- \( 2 \cdot ((3 \cdot 4) \cdot (5 + 1)) \)
- \( 2 \cdot ((3 \cdot 4) \cdot ((5 + 1)) \cdot 5) \)
- \( 2 \cdot ((3 \cdot 4) \cdot ((5 + 1) \cdot 5)) \)
- \( ((2 \cdot 3) \cdot (4 \cdot (5 + 1))) + 1 \)
- \( ((2 \cdot 3) \cdot ((4 \cdot 5) + 1)) + 1 \)
- \( ((2 \cdot 3) \cdot ((4 \cdot 5) + 1)) \cdot 5 \)
### Conclusion:
By evaluating the expression for all possible placements of parentheses, we find that there are \( 14 \) distinct values that can be obtained. Therefore, the final answer is:
\[
\boxed{14}
\]
Correct Answer: 4Not great! Can we do better? We’d like to see more coherent and concise reasoning traces, which should also lead to more accurate answers. Let’s use —-n 16 to sample 16 outputs from the base model for each prompt, and select the best one based on the rewards from the PRM:
python bon.py --base_model Qwen/Qwen2.5-1.5B-Instruct --prm_model axolotl-ai-co/Qwen2.5-Math-PRM-7B --n 16 --num_gpus 2You should see something like the following output:
================================================================================
Problem: Define \[p = \sum_{k = 1}^ \infty \frac{1}{k^2} \quad \text{and} \quad q = \sum_{k = 1}^\infty \frac{1}{k^3}.\]Find a way to write \[\sum_{j = 1}^\infty \sum_{k = 1}^\infty \frac{1}{(j + k)^3}\] in terms of $p$ and $q.$
Predicted answer (BoN): To solve the given problem, we need to express the double sum \(\sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3}\) in terms of \(p\) and \(q\).
First, let's rewrite the double sum by changing the order of summation. We start by summing over \(m = j + k\). For a fixed \(m\), \(j\) and \(k\) can take any values from 1 to \(\infty\) such that \(j + k = m\).
The number of pairs \((j, k)\) that satisfy \(j + k = m\) is \(m-1\). Therefore, we can express the sum as:
\[
\sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3} = \sum_{m=1}^\infty \frac{m-1}{m^3}.
\]
To evaluate this sum, we can split it into two separate sums:
\[
\sum_{m=1}^\infty \frac{m-1}{m^3} = \sum_{m=1}^\infty \left( \frac{m}{m^3} - \frac{1}{m^3} \right) = \sum_{m=1}^\infty \left( \frac{1}{m^2} - \frac{1}{m^3} \right).
\]
This can be further simplified into two separate sums:
\[
\sum_{m=1}^\infty \frac{1}{m^2} - \sum_{m=1}^\infty \frac{1}{m^3} = p - q.
\]
Thus, the original sum can be expressed in terms of \(p\) and \(q\) as:
\[
\sum_{j=1}^\infty \sum_{k=1}^\infty \frac{1}{(j+k)^3} = p - q.
\]
Therefore, the final answer is:
\[
\boxed{p - q}.
\]
Correct Answer: p - q
================================================================================
Problem: A regular hexagon can be divided into six equilateral triangles. If the perimeter of one of the triangles is 21 inches, what is the perimeter, in inches, of the regular hexagon?
Predicted answer (BoN): ## Step 1:**
First, let's understand that a regular hexagon can be divided into six equilateral triangles. The perimeter of one of these triangles is given as 21 inches. Since all sides of an equilateral triangle are equal, each side of the triangle must be 21 inches divided by 3, as it's equal to the perimeter divided by 3.
**Calculation for one side of the triangle:**
\[ \text{Side length of the triangle} = \frac{21}{3} = 7 \text{ inches} \]
## Step 2:**
Now, since the hexagon is made up of these equilateral triangles, each side of the hexagon will be equal to the side length of one of these triangles. Therefore, the perimeter of the hexagon, which is the sum of all its sides, will be six times the side length of one of the triangles.
**Calculation for the perimeter of the hexagon:**
\[ \text{Perimeter of the hexagon} = 6 \times 7 \]
## Step 3:**
Perform the multiplication to find the final perimeter.
\[ \text{Perimeter of the hexagon} = 6 \times 7 = 42 \text{ inches} \]
Therefore, the final answer is: $\boxed{42}$.
Correct Answer: 42
================================================================================
Problem: The expression $2\cdot 3 \cdot 4\cdot 5+1$ is equal to 121, since multiplication is carried out before addition. However, we can obtain values other than 121 for this expression if we are allowed to change it by inserting parentheses. For example, we can obtain 144 by writing \[ (2\cdot (3\cdot 4)) \cdot (5+1) = 144. \]In total, how many values can be obtained from the expression $2\cdot 3\cdot 4 \cdot 5 + 1$ by inserting parentheses? (Note that rearranging terms is not allowed, only inserting parentheses).
Predicted answer (BoN): To solve the problem of determining how many different values can be obtained from the expression \(2 \cdot 3 \cdot 4 \cdot 5 + 1\) by inserting parentheses, we need to consider the different ways we can group the terms using parentheses. Since multiplication is carried out before addition, we need to consider all possible ways we can group the numbers \(2\), \(3\), \(4\), and \(5\) using parentheses.
First, let's list all possible combinations of parentheses groups. Each group will have a different number of terms inside them. The possible groups are:
1. \(2, 3, 4, 5\)
2. \(2, 3 \cdot 4, 5\)
3. \(2, 3 \cdot (4 \cdot 5)\)
4. \(2 \cdot 3, 4, 5\)
5. \(2 \cdot 3 \cdot 4, 5\)
6. \(2 \cdot 3 \cdot (4 \cdot 5)\)
7. \(2, (3 \cdot 4) \cdot (5 + 1)\)
8. \(2 \cdot (3 \cdot 4), 5 + 1\)
9. \(2 \cdot (3 \cdot (4 \cdot 5))\)
10. \(2 \cdot (3 \cdot (4 \cdot (5 + 1)))\)
Now, let's evaluate each of these groups:
1. \(2, 3, 4, 5\) : This evaluates to \(2 \cdot 3 \cdot 4 \cdot 5 + 1 = 121\).
2. \(2, 3 \cdot 4, 5\) : This evaluates to \(2 \cdot (3 \cdot 4) + 5 = 2 \cdot 12 + 5 = 29\).
3. \(2, 3 \cdot (4 \cdot 5)\) : This evaluates to \(2 \cdot (3 \cdot 20) + 1 = 2 \cdot 60 + 1 = 121\).
4. \(2, 3 \cdot (4 \cdot 5)\) (repeated, but valid) : This is equivalent to the third case, evaluating to 121.
5. \(2, 3 \cdot (4 \cdot 5)\) : This is equivalent to the third case, evaluating to 121.
6. \(2, (3 \cdot 4) \cdot (5 + 1)\) : This evaluates to \(2 \cdot (12 \cdot 6) + 1 = 2 \cdot 72 + 1 = 145\).
7. \(2 \cdot (3 \cdot 4), 5 + 1\) : This evaluates to \(2 \cdot (12) + 6 = 2 \cdot 12 + 6 = 30\).
8. \(2 \cdot (3 \cdot (4 \cdot 5))\) : This evaluates to \(2 \cdot (3 \cdot 20) + 1 = 2 \cdot 60 + 1 = 121\).
9. \(2 \cdot (3 \cdot (4 \cdot 5))\) (repeated, but valid) : This is equivalent to the eighth case, evaluating to 121.
10. \(2 \cdot (3 \cdot (4 \cdot (5 + 1)))\) : This evaluates to \(2 \cdot (3 \cdot (4 \cdot 6)) + 1 = 2 \cdot (3 \cdot 24) + 1 = 2 \cdot 72 + 1 = 145\).
From the above evaluations, we see that the distinct values obtained are 121, 145, and 30. Therefore, the number of different values that can be obtained from the expression \(2 \cdot 3 \cdot 4 \cdot 5 + 1\) by inserting parentheses is \(\boxed{3}\).
Correct Answer: 4Much better! You can experiment with different values of n here - larger values should improve the accuracy of model outputs.
Thanks so much for reading. We hope you enjoy using this new feature, and we’d love to see the wonderful things that you produce with it - share your work with us on our Discord or Twitter!
Acknowledgements
Thanks to the TRL library for enabling support for PRM training, which we use to power our PRM training functionality.
Thanks to the Hugging Face team for open-sourcing their work on test-time compute - our evaluations section would be incomplete without it.